K-minimum spanning tree

In mathematics, given an undirected graph 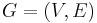G=(V,E) with non-negative edge costs and an integer k , the k -minimum spanning tree, or k -MST, of G is a tree of minimum cost that spans exactly k vertices of G . A k -MST does not have to be a subgraph of the minimum spanning tree (MST) of G . This problem is also known as Edge-Weighted k -Cardinality Tree (KCT).

The k-MST problem is shown to be NP-Hard by reducing the Steiner tree problem to the k -MST problem. There are many constant factor approximations for this problem. The current best approximation is a 2-approximation due to Garg. This approximation relies heavily on the primal-dual schema of Goemans and Williamson.

When the k -MST problem is restricted to the Euclidean plane, there exists a PTAS due to Arora.

Refer to KCTLIB for more information.

References

  • Arora, S. (1998), "Polynomial time approximation schemes for euclidean traveling salesman and other geometric problems.", J. ACM .
  • Garg, N. (2005), "Saving an epsilon: a 2-approximation for the k-MST problem in graphs.", STOC .
  • Ravi, R.; Sundaram, R.; Marathe, M.; Rosenkrantz, D.; Ravi, S. (1996), "Spanning trees short or small", SIAM Journal of Discrete Mathematics .
  • Goemans, M.; Williamson, P. (1992), "A general approximation technique for constrained forest problems", SIAM Journal on Computing .

External links